蒙特·卡罗方法（Monte Carlo method），也称统计模拟方法，是一种以概率统计理论为指导的数值计算方法。当所求解问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种“实验”的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解。很明显，它是一种使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。蒙特卡罗方法于20世纪40年代美国在第二次世界大战中研制原子弹的“曼哈顿计划”计划的成员John von Neumann, Stanislaw Ulam和Nicholas Metropolis首先提出。为象征性地表明这一方法的概率统计特征，数学家Neumann用驰名世界的赌城—摩纳哥的Monte Carlo—来命名这种方法。

    蒙特卡罗方法的解题过程可以归结为三个主要步骤：（1）构造或描述概率过程：对于本身就具有随机性质的问题，主要是正确描述和模拟这个概率过程，对于本来不是随机性质的确定性问题，就必须事先构造一个人为的概率过程，即要将不具有随机性质的问题转化为随机性质的问题；（2）实现从已知概率分布抽样:由于各种概率模型都可以看作是由各种各样的概率分布构成的，因此产生已知概率分布的随机变量（或随机向量），就成为实现蒙特卡罗方法模拟实验的基本手段，这也是蒙特卡罗方法被称为随机抽样的原因。（3）建立各种估计量：构造了概率模型并能从中抽样后，即实现模拟实验后，我们就要确定一个随机变量，作为所要求的问题的解。建立各种估计量，相当于对模拟实验的结果进行考察和登记，从中得到问题的解。

    从理论上来说，蒙特卡罗方法中执行的实验次数越多，所得到的结果才越精确。计算机技术的发展，使得蒙特卡罗方法在最近10年得到快速的普及。现代的蒙特卡罗方法，已经不必亲自动手做实验，而是借助计算机的高速运转能力，使得原本费时费力的实验过程，变成了简单而快速的事情。

    蒙特卡罗方法有很强的适应性，问题的几何形状的复杂性对它的影响不大。该方法的收敛性是指概率意义下的收敛，因此问题维数的增加不会影响它的收敛速度，而且存贮单元也很省，这些是用该方法处理大型复杂问题时的优势。因此，随着电子计算机的发展和科学技术问题的日趋复杂，蒙特卡罗方法的应用也越来越广泛。

    随着全球能源逐渐趋于紧张以及国家能源战略的逐步实施，对石油探测提出了越来越高的要求。目前，利用核探测技术进行油田测井已经比较普遍。核探测技术的基本原理是用高能中子照射被探测物品，中子与被探测物品作用产生非弹，探测器通过接受到的信息来推测被探测物品的元素含量，确定地层矿物成分。

    C/O碳氧比能谱测井是通过测量脉冲中子在地层中激发的非弹性射线的能谱来确定淡水油田套管井外地层中含油饱和度的一种测井方法。具体来说就是测量中子与C、O、Si及Ca等原子核非弹性散射发出的能谱。它使用脉冲式D-T反应产生的14 MeV中子源，由脉冲中子发生器产生的中子入射到地层后，在最初极短时间内（约10-2到10-1s）将与地层中各种元素的原子核发生非弹性散射，损失大量能量，同时发出非弹性射线。以C、O为例，最突出的射线峰分别为4.43 MeV和6.13 MeV。除了非弹性射线外，14 MeV中子进入地层后还会发出俘获射线和活化射线。测井仪采用脉冲中子源技术，利用上述三种辐射完全不同的时间特征，采用与中子脉冲同步测量技术，通过扣除本底谱办法获取非弹性散射净谱。

    石油探测主要感兴趣的地质参数有体积密度、孔隙度和岩性。设计的各种核探测仪也直接或间接用于测量这些参数。用数值模拟方法预测测井仪响应在实际测井中是十分有用的，首先因为数值模拟成本低，并且实验不可能给出岩层及井眼环境孤立的、定量的数值变化，其次数值模拟可减少建模型井的数量和费用，还可给出仪器效应对探测器计数的影响，有助于仪器设计和刻度。由于核测井涉及的问题多、难度大，对计算方法和软件都是一大挑战。

    MCCO（碳氧比能谱测井的蒙特卡罗模拟平台）就是这么一款数值模拟软件，使用蒙特卡洛模拟的方法来预测C/O碳氧比能谱，从而达到油田测井的目的，可以节约石油探测的费用，提高探测开发速度。该软件使用到的计算C/O碳氧比能谱的公式为：
 

 

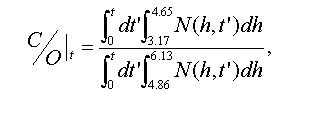
    利用该软件，对两个油井探测过程中的常见情景：孔隙度均为35％的(1)饱和水砂(SiO2+H2O)和(2)饱和油砂(C16H34+SiO2)，进行蒙特卡洛模拟，计算进入探测器的次级流，使用的模型如下图所示：

 

 

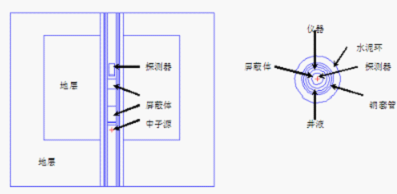
    通过模拟计算,得到的结果如表1和2所示：

 

 

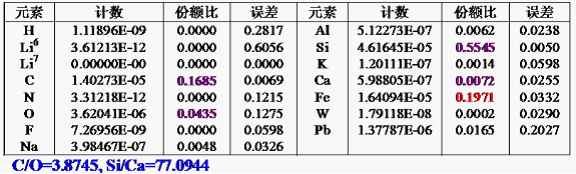
表2饱和油砂各元素瞬发计数

   
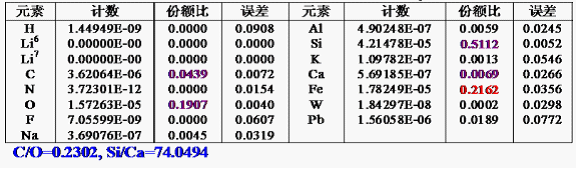
    除此之外，该软件还曾经完成隐藏爆炸物的探测，也得到了较为理想的结果。